En un mundo donde los datos son omnipresentes, la habilidad para interpretarlos correctamente es más crucial que nunca. La «ceguera estadística» es un fenómeno preocupante, donde la mala interpretación de datos estadísticos puede llevar a conclusiones erróneas y decisiones mal informadas. Este texto tiene como objetivo desmitificar este concepto y proporcionar ejemplos claros para una mejor comprensión.

 

¿Qué es la Ceguera Estadística?

La ceguera estadística ocurre cuando las personas no logran interpretar, analizar o entender adecuadamente los datos estadísticos. Este fenómeno puede ser resultado de una presentación engañosa de los datos, falta de contexto, sesgo de confirmación, errores en la interpretación de correlaciones y causalidades, o una sobresimplificación de la información.

 

1. Gráficos Engañosos:

Caso: ¡Aumentamos las gráficas significativamente!

Problema: Eje y no comienza en cero, creando una impresión de cambio dramático.

Solución: Siempre verifique la escala de los ejes en los gráficos.

Ejemplo: Gráfico Engañoso

 

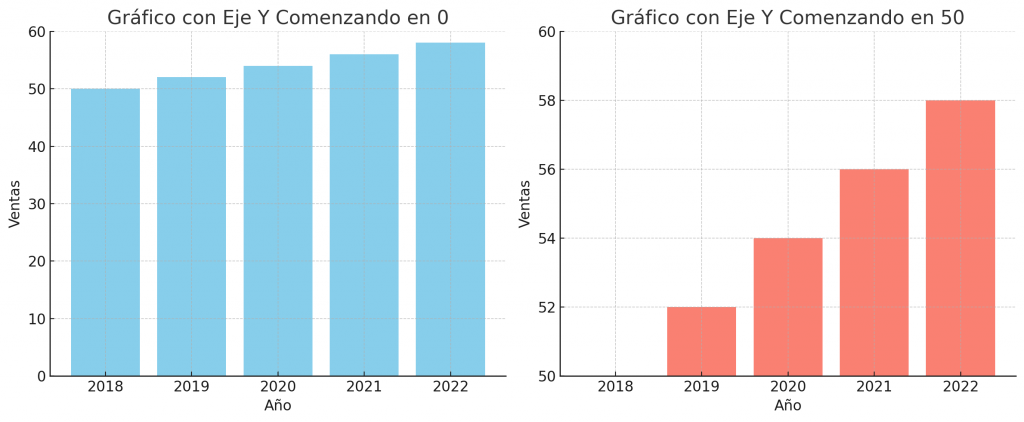
Esta imagen muestra dos gráficos de barras representando las mismas ventas a lo largo de los años, pero con diferentes escalas en el eje y.

Izquierda: El gráfico con el eje y comenzando en 0 muestra un incremento leve y proporcional en las ventas a lo largo del tiempo.
Derecha: El gráfico con el eje y comenzando en 50, aunque muestra los mismos datos, da la impresión de un aumento mucho más dramático en las ventas.

Este ejemplo ilustra cómo la elección de la escala en un gráfico puede influir significativamente en la percepción de los datos.

 

2. Correlación vs. Causalidad:

Caso: ¡Las Heladerías son culpables de los crímenes!

Problema: Interpretación errónea de que las heladerías causan crimen.

Solución: Entender que correlación no implica causalidad; buscar factores comunes subyacentes.

Ejemplo: Aquí tienes una representación gráfica que ilustra el ejemplo de «Correlación vs. Causalidad» en el contexto de heladerías abiertas y crímenes reportados:

 

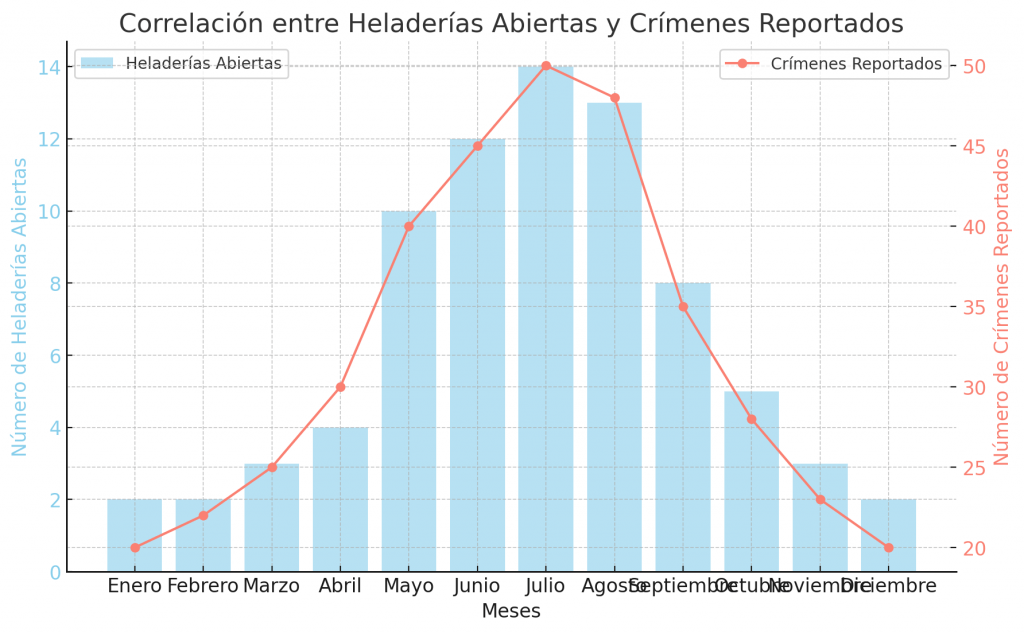
En este gráfico, se observa una correlación entre el número de heladerías abiertas (barras azules claras) y el número de crímenes reportados (línea roja) a lo largo de los meses del año. Ambos aumentan durante los meses de verano y disminuyen en invierno.

Sin embargo, este gráfico sólo muestra una correlación y no implica causalidad. Es decir, el aumento en el número de heladerías abiertas no causa necesariamente un aumento en los crímenes. En cambio, ambos fenómenos pueden estar relacionados con un factor común subyacente, como el clima más cálido en el verano, que influye tanto en la apertura de heladerías como en un posible incremento en la actividad al aire libre y, por ende, en los crímenes reportados.

Este ejemplo demuestra la importancia de no sacar conclusiones apresuradas sobre la causalidad basándose únicamente en correlaciones observadas.

 

 

3. Porcentajes Sin Contexto:

Caso: Informe indica un aumento del 50% en una enfermedad.

Problema: Sin saber que es un aumento de 2 a 3 casos, suena alarmante.

Solución: Buscar siempre el contexto numérico detrás de los porcentajes.

Ejemplo: Esta representación gráfica ilustra el concepto de «Porcentajes Sin Contexto» utilizando el ejemplo de un informe sobre el aumento de una enfermedad

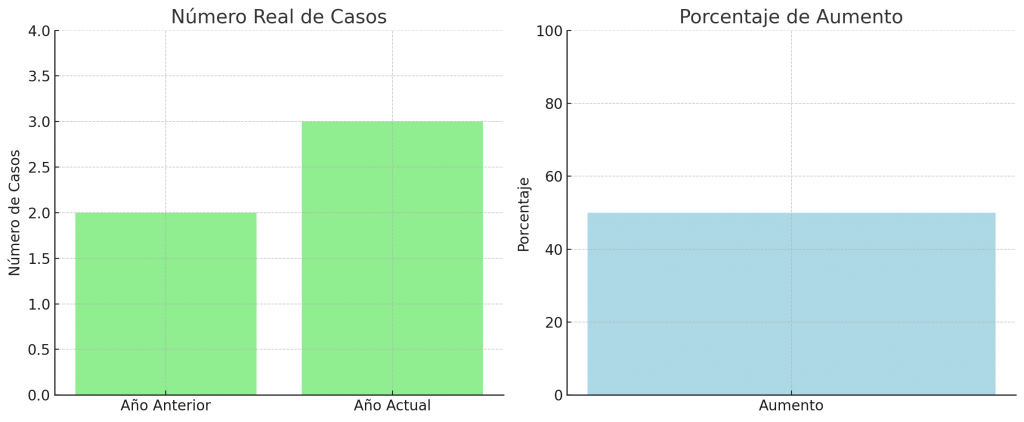
Izquierda: El primer gráfico muestra el número real de casos de la enfermedad en dos períodos diferentes: el «Año Anterior» y el «Año Actual». Aquí, se ve un cambio de 2 a 3 casos, lo cual es un aumento, pero la magnitud es pequeña.

Derecha: El segundo gráfico muestra el porcentaje de aumento, que es del 50%. Aunque este porcentaje parece significativo, al observar el número real de casos, se hace evidente que el cambio es mínimo.

Este ejemplo demuestra cómo los porcentajes pueden ser engañosos sin el contexto adecuado. Un aumento del 50% suena alarmante, pero al ver los números reales, se comprende que el cambio es, de hecho, muy pequeño. Por lo tanto, es esencial buscar el contexto numérico detrás de los porcentajes para obtener una comprensión precisa de lo que representan.

 

4. Sesgo de Confirmación:

Caso: Inversor ignora datos de recesión, enfocándose solo en los positivos.

Problema: Sesgo hacia datos que confirman creencias preexistentes.

Solución: Considerar todas las fuentes de datos relevantes, evitando prejuicios personales.

Ejemplo: Esta representación gráfica ilustra el ejemplo de «Sesgo de Confirmación» en el contexto de un inversor que se enfoca solo en datos económicos positivos, ignorando los negativos

 

 

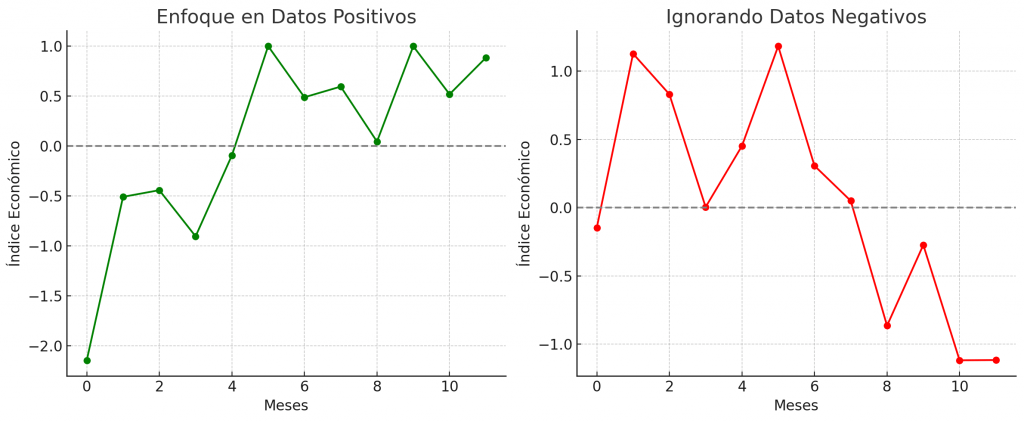
Izquierda: El primer gráfico muestra una serie de datos económicos con una tendencia general positiva (en verde). Este gráfico podría representar la perspectiva de un inversor que solo presta atención a los datos que muestran una tendencia económica al alza, confirmando su creencia o deseo de que el mercado está mejorando.

Derecha: El segundo gráfico presenta la misma serie de datos, pero con una tendencia general negativa (en rojo). Este gráfico podría ser ignorado por el inversor, ya que contradice su visión optimista del mercado.

Ambos gráficos utilizan los mismos datos subyacentes, pero la interpretación y el enfoque en una tendencia específica (positiva o negativa) pueden cambiar drásticamente la percepción del estado de la economía. Este ejemplo muestra cómo el sesgo de confirmación puede llevar a una interpretación parcial y potencialmente engañosa de los datos económicos. La solución es considerar todas las fuentes de datos relevantes y evitar prejuicios personales para obtener una visión más equilibrada y precisa.

 

5. Sobresimplificación:

Caso: Concluir que el dinero no influye en la felicidad basado en una encuesta.

Problema: Ignorar la complejidad y múltiples factores que afectan la felicidad.

Solución: Evitar reducir datos complejos a generalizaciones simples.

Ejemplo: El gráfico de dispersión representa los ingresos de los individuos en el eje x y sus niveles auto-reportados de felicidad en el eje y. Cada punto representa a una persona, con el color indicando su nivel de felicidad.

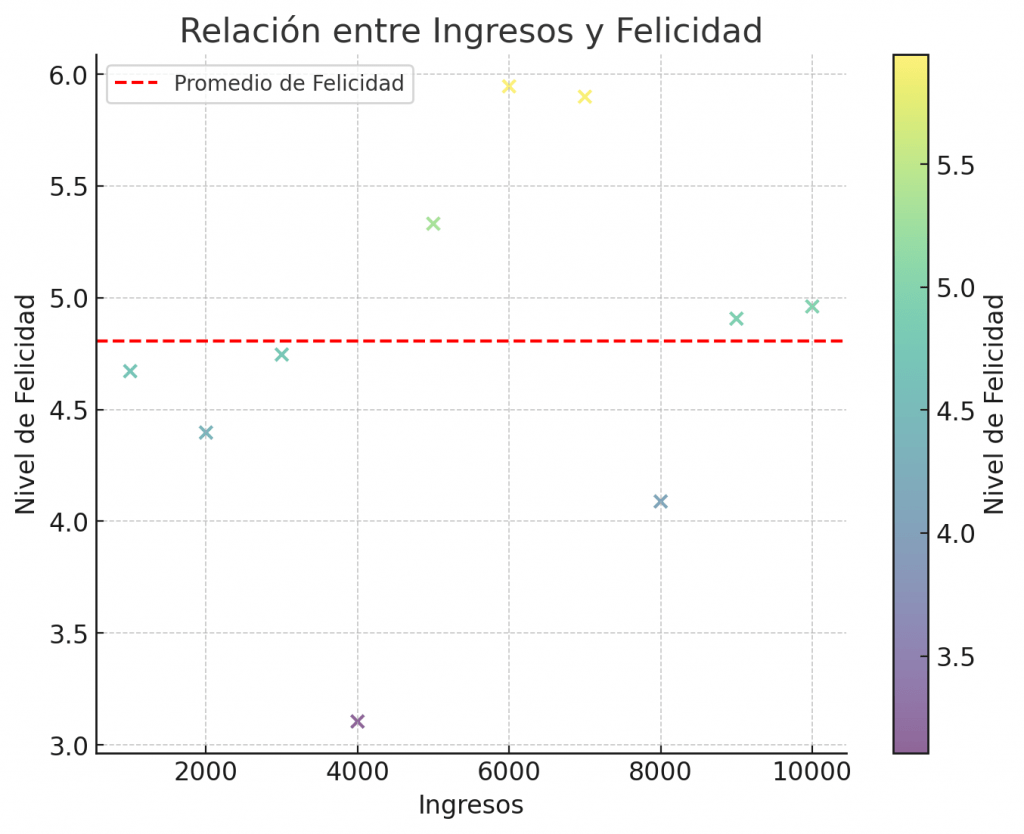
Observación Clave: Aunque podría parecer que no hay una relación fuerte entre ingresos y felicidad (dada la dispersión de los puntos y la línea roja que muestra el promedio de felicidad), esta vista simplifica en exceso la realidad.

Este ejemplo demuestra cómo la sobresimplificación puede llevar a conclusiones erróneas. La felicidad es un concepto multifacético influenciado por muchos factores además de los ingresos, como la salud, las relaciones personales, el entorno, entre otros. Al mirar solo los ingresos, se ignora la complejidad y los múltiples factores que afectan la felicidad.

La solución es evitar reducir los datos complejos a generalizaciones simples y considerar la variedad de factores que pueden influir en los resultados de una encuesta o estudio. Esto proporciona una comprensión más completa y matizada de los datos.

 

Ten Cuidado:

Ten cuidado de la gente que hace uso de esta ceguera en la que fácilmente todos cabemos. Lo hacen políticos, economistas y todos los que quieren usar datos para que creamos en algo que es mentira.

Los datos son una herramienta poderosa. Pueden iluminar verdades y revelar patrones ocultos, pero también pueden ser manipulados para engañar y confundir. La ceguera estadística, la dificultad para interpretar correctamente los datos, es un terreno fértil para aquellos que buscan influir en la opinión pública con fines propios. Es crucial ser consciente de cómo políticos, economistas y otros actores pueden hacer uso de esta ceguera para promover agendas que pueden no ser completamente honestas.

Los políticos, por ejemplo, a menudo usan estadísticas para respaldar sus argumentos o políticas. Pueden seleccionar convenientemente datos que apoyen su punto de vista, ignorando aquellos que no lo hacen. Esto puede incluir presentar porcentajes sin el contexto adecuado, utilizar gráficos engañosos, o interpretar de manera errónea las correlaciones como si fueran causas.

Los economistas y analistas de mercado, por su parte, pueden caer en la trampa de la sobresimplificación. Al reducir complejas realidades económicas a tendencias o patrones simples, pueden ofrecer una visión distorsionada de la economía que favorece ciertos intereses económicos o políticos.

La clave para defendernos contra la manipulación a través de la ceguera estadística es el escepticismo saludable y la educación. Aprender los fundamentos de la estadística y el análisis crítico de datos es esencial. Además, es importante buscar información de múltiples fuentes y estar abierto a diferentes perspectivas.

 

Consejos para Evitar la Ceguera Estadística

1. Educación en Estadística: Un conocimiento básico de estadística es esencial.
2. Pensamiento Crítico: Acercarse a los datos con una mente analítica y cuestionadora.
3. Buscar Contexto: Comprender el trasfondo de los datos.
4. Verificar Fuentes: Considerar la fuente de los datos y su fiabilidad.
5. Consultar Expertos: En caso de duda, buscar la opinión de especialistas en el área.

 

Conclusión

La ceguera estadística no es solo un problema para científicos o analistas de datos, sino que afecta a todos en la era de la información. Entender y reconocer este fenómeno es el primer paso para tomar decisiones informadas y basadas en datos. Al aplicar los consejos mencionados y acercarse a los datos con un análisis crítico, podemos evitar caer en las trampas de la interpretación errónea y utilizar la información estadística para mejorar nuestras vidas y nuestro entorno.